Resolución Lógica:

En programación lógica se utiliza una única regla: la regla de resolución.

Utilizando esta regla y la demostración por reducción al absurdo podemos demostrar cualquier teorema dentro del subconjunto de lógica de predicados que tratamos (las cláusulas de Horn).

Vamos a ver la regla de resolución aplicada primero a lógica proposicional, y después la veremos ya aplicada a lógica de predicados.


Regla de resolución

Reglas habituales:

Ejemplo de refutación por resolución

Refutación de {{p, q}, {¬p, q}, {p, ¬q}, {¬p, ¬q}} :
      1 {p, q} Hipótesis
      2 {¬p, q} Hipótesis
      3 {p, ¬q} Hipótesis
      4 {¬p, ¬q} Hipótesis
      5 {q} Resolvente de 1 y 2
      6 {¬q} Resolvente de 3 y 4
      7 Resolvente de 5 y 6

Algoritmo de de resolución por saturación 

Def.: Sea S un conjunto de cláusulas.
         Res(S) = S ∪ ( S {Res(C1, C2) : C1, C2 ∈ S}).

Algoritmo de resolución por saturación

Entrada: Un conjunto finito de cláusulas, S.
Salida: Consistente, si S es consistente;
            Inconsistente, en caso contrario.

S 0 := ∅
mientras ( 6∈ S) y (S 6= S 0) hacer
       S 0 := S
       S := Res(S)
fmientras
si ( ∈ S) entonces
    Devolver Inconsistente
en caso contrario
    Devolver Consistente
fsi

Prop.: El algoritmo de resolución por saturación es correcto.

Programa para solucionar resolución:

Sin resultado de programas para la solucion de resoluciones logicas.


Bibliografia:

http://informatica.uv.es/iiguia/MD/prog_log3.pdf
https://www.cs.us.es/~jalonso/cursos/li-12/temas/tema-5.pdf

Deducción natural

El metodo de deduccion natural, desarrollado por Gentzen, utiliza dos reglas de inferencia por cada conectiva: una para insertar la conectiva y otra para eliminarla

Las reglas de inferencia son:

A continuacion se incluyen varios ejemplos de demostraciones en deducion natural.

Para que sirve:

La deducción natural sirve para intentar demostrar que un razonamiento es correcto (``para comprobar la validez de un secuente'', dice la teoría). Ejemplo:
Yo te digo: ``En verano hace calor, y ahora estamos en verano, por eso hace calor''. Tú te pones a hacer cálculos, y respondes ``Vale, puedo demostrar que el razonamiento que has hecho es correcto''. Para eso sirve la deducción natural.


Programas para la deducion natural

Sin resultados al momento de encontrar un programa para calcular la deduccion natural.

Bibliográfia: 

http://di002.edv.uniovi.es/~labra/Logica/apuntes/nd.pdf

http://www.danielclemente.com/logica/dn-node12.html

TEMA TABLEAUX (Tableros semánticos).

TABLEROS SEMÁNTICOS

Las tablas o árboles semánticos son un mecanismo de decisión para sentencias de un lenguaje formal. Aunque se puede decir que los procedimientos tabulares comienzan con Gentzen (en 1935). Se considera a Beth el creador del procedimiento de árboles semánticos, destacando su “Semantic entailment and formal derivability”.Beth la define como un intento de búsqueda sistemática de contra ejemplos para determinar si una fórmula es consecuencia lógica de otras.

Este método se utiliza para verificar la satisfacibilidad de una fórmula proposicional. 

Para implementar este metodo o algoritmos es necesario tener en cuenta los siguientes y muy importantes fundamentos:

Literales y formulas complementarias.

Un literal es una variable proposicional o la negación de una variable proposicional, por ejemplo p, ¬q, s, ¬t son literales. Un conjunto de literales es satisfacible si y sólo si no contiene un par complementario de literales.

1-      Si p es un átomo,{p, ¬p} son una pareja complementaria de literales.

Si se asigna v(p) = V entonces v(¬p) = F, si se asigna v(p) = F entonces v(¬p) = V.

2-      Si A es una fórmula, {A,¬A} es un par complementario de fórmulas A es el complemento de ¬A y viceversa.

Para el caso de las fórmulas por ejemplo si se tiene: v(p → q) = V, entonces su complemento es:  v(¬(p → q)) = F.

Método de los Tableros semánticos

Este método realiza una búsqueda sistemática de modelos, disminuyendo la satisfacibilidad de toda fórmula a la de algunos literales de la misma.

Considere la fórmula A: (p v ¬q). El conjunto de literales es: {p, ¬q} se tiene que no es un par complementario de literales, por lo tanto se puede establecer un modelo para la fórmula A: v(p) = V, v(q)= F. La fórmula (p v ¬q) es satisfacible.

Si se tiene la fórmula A: (p & q) → ¬r. el conjunto de literales es: {p, q, ¬r} se tiene que no es un par complementario de literales, por lo tanto se puede establecer un modelo para la fórmula A: v(p) = V, v(q)= F v(¬r) = V. La fórmula (p & q) → ¬r es satisfacible.

Dada la fórmula A: (p & ¬p) .entonces v(A) = V si y solo si v(p) = V y v(¬p) =  V  para este caso se tiene el conjunto de literales es : {p, ¬p} este conjunto tiene un par complementario de literales, y podemos afirmar que no se puede encontrar un modelo para la fórmula A, es decir que A es insatisfacible.

De lo anterior se puede afirmar que un conjunto de literales es satisfacible si y solo si no contiene un par complementario de literales.

Considere la fórmula A: p & (p v ¬p) , A es verdadera si v(q) = V y v(p v ¬q) = V. Entonces v(A) = V, si:

            1. v(q) = V y v(p) = V o

            2. v(q) = V y v(¬q) = V

La satisfacibilidad para una fórmula A queda asociada a la satisfacibilidad de un conjunto de literales.

En el anterior ejemplo tenemos el primer conjunto de literales {q, p} y se observa que no es un par complementario lo que nos permite afirmar que el conjunto es satisfacible y se puede establecer un modelo para la fórmula A, el cual es: v(q) =V y v(p) = V, por lo tanto la fórmula es satisfacible. El segundo conjunto de literales {q, ¬q} es un par complementario, este conjunto no es satisfacible y no se puede encontrar un modelo

Fórmulas alfa (α) y beta (β).

Hay dos tipos de reglas:

1-Las α que son conjuntivas y estas satisfacen si y sólo si ambas fórmulas α₁ y α₂ son satisfacibles.

2-Las β que son disyuntivas y estas satisfacen si al menos una de las fórmulas β₁ y β₂ son satisfacibles.

Las fórmulas alfa, junto con sus componentes son:

-Si F es alfa con componentes F₁ y F₂ entonces F ≡ F₁  ᴧ  F₂.

Las fórmulas beta, junto con sus componentes son:

-Si F es alfa con componentes F₁ y F₂ entonces F ≡ F₁  v  F₂.

Definiciones:

1-      Una rama de un árbol de verdad es cerrada si y sólo si contiene una formula y su negación.

2-      Una rama de un árbol de verdad es abierta si y sólo si contiene fórmulas descompuestas atómicas y sus negaciones.

3-      Un árbol de verdad es abierto si y sólo si contiene al menos una rama completa abierta.

4-      Un árbol de verdad es cerrado si y sólo si todas sus ramas son cerradas.

5-      Una fórmula es satisfacible si y sólo si tiene un árbol de verdad abierto.

Ejemplo tablero semántico.

Búsqueda exitosa de modelos de modelos por tableros semánticos.

Búsqueda fallida de modelos por tableros semánticos.

DIAGRAMA DE CLASES

DIAGRAMA DE FLUJO

BIBLIOGRÁFICA

Blog base y muy completo para saber sobre este tema:

http://logicaftablerossemanticos.blogspot.com.co/2014/10/tableros-semanticos-las-tablas-o.html

TALLER #4

Método analítico 

Este método consiste en comparar la forma o estructura de la inferencia que se quieres analizar con otra lógicamente valida.

Programas para solucionar tablas de verdad 

AnallogicA

Es una aplicación diseñada para generar tablas de verdad a partir de proposiciones lógicas.

Este programa admite hasta 15 variables diferentes, lo que en combinaciones serian mas de 32000 posibilidades.

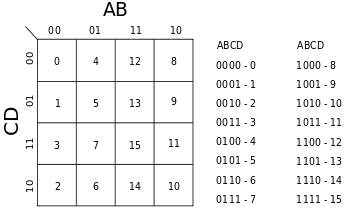
GKmap

Pueden ser utilizados en la simplificación de sentencias definidas en lógica Booleana.

Este programa admite variables de entrada de 16 formas diferentes.

Multisim 

Es una gran herramienta para el análisis de circuitos digitales. Puede crear una tabla de verdad o expresión Booleana a partir de un circuito digital o bien producir un circuito desde una tabla de verdad o expresión Booleana.

Este programa admite hasta 8 variables diferentes de entrada.

Programas para calcular método abreviado y analógico

Búsquedas incompletas debido a no encontrar programas que me calculen dichos métodos de la lógica proposicional.

Implicación

La implicación es una estructura en donde una proposición es consecuencia lógica de otra. La forma de representarla correctamente es P => Q, y se lee “P implica lógicamente a Q” o “Q es una implicación lógica de P”. 
Por otra parte se puede leer esta estructura como “Si P entonces Q”. El significado es que la proposición de la izquierda es verdadera, entonces la proposición de la derecha es verdadera.

Implicación directa

La implicación directa es p -->q 

Es decir, "si p entonces q". 


Implicación reciproca 

Dada la proposición condicional p -->q se define:

La implicación reciproca es q-->p

Es decir "Si q entonces p"


Implicación contra reciproca

Dada la proposición condicional p -->q se define:

La implicación contra reciproca es ¬q --> ¬p

Es decir "Si ¬q entonces ¬p"


Implicación Inversa 

Dada la proposición condicional p -->q se define:

La implicacion inversa es ¬p --> ¬q

Es decir "Si ¬p entonces ¬q"




¿QUE ES?


Tautologia

Son identidades logicas que siempre seran verdaderas, son principalmente usadas para pruebas senteciales desempeñan un papel fundamental en el metodo de deducion 

1. Voy a bajar abajo.
2. Rió a carcajadas del chiste.
3. Proyectando al futuro.
4. Lo estoy viendo con mis propios ojos.
5. Celebrando la fiesta.
6. La madrugada llegó muy temprano.
7. Veré una película en el cine. 

Satisfactibilidad
Una fórmula proposicional es satisfacible si toma el valor T para alguna interpretacion • Una formula proposicional es insatisfacible si no es satisfacible, e.d. si su valor es F para todas las interpretaciones, e.d. si es una contradicción.

- Una formula A es tautología (valida) si y solo si ¬A es insatisfacible 
- A es satisfacible si y solo si ¬A es falsificable. 
- A es falsificable si existe una interpretacion que hace que A valga F


Consistencia

Es decir, si existe al menos una interpretación que haga verdaderas a todas las fórmulas del conjunto. En términos sintácticos, un conjunto de fórmulas es consistente si y sólo si para toda fórmula A, no es posible deducir tanto A como ￢A (i.e. la negación lógica de A) a partir del conjunto de fórmulas.



MÉTODO ABREVIADO.



¿Para que sirve?

El metodo abreviado sirve para simplificar el uso de la tabla de valores para lo cual se debe seguir un conjunto de reglas.

1. Suponer que la conclusion es FALSA.

2. Suponer que todas las premisas son VERDADERAS.

3. Partiendo de la conclusion, se determinan los valores de verdad de p, q y r.

4. Los valores de verdad hallados en la conclusion se trasladan a la primera premisa de preferencia, y luego a la segunda, tercera, etc.

5. Si los valores de verdad de p, q, r toman un solo valor, la inferencia No es valida.

6. Basta que una de las variables ( p, q, r ) tomen dos valores de verdad, entonces la inferencia es valida 




Algoritmo

1. Se supone verdadero el consecuente y falso el consecuente

2. se determinan los valores de las variables del consecuente de manera que expresen la falsedad de este

3: Se transladan estos valores al antecedente y se designan los valores de las demas variables tratando de hacer verdadero el antecedente

4. Si se verifica la hipotesis, la formula es no tautologica, en consecuencia, la inferencia correspondiente sera invalida; si no se verifica la hipotesis, la formula sera tautologica, en consecuencia, la inferencia correspondiente sera valida.

Ejemplo

Sea la inferencia

Si eres fiscal eres abogado. Si eres profesional, Eres abogado.Luego, Si eres Fiscal, eres profesional

Formula

Procedimiento

a) Se supone V (verdadero el antecedente y F (falso) el consecuente:

b) Se detemina el valor de las variables del consecuente

c) Se Transladan estos valores el antecedente y se asignan los valores a las demas variables:

d) habiendo asignado el valor de verdad de V a la variable q, las dos premisas han asumido el valor de verdad y todo el antecedente ha tomado el valor de verdad con lo que queda verificada la hipotesis siendo, por lo tanto , la formula no tautologica; es decir, la inferencia correspondiente invalida.